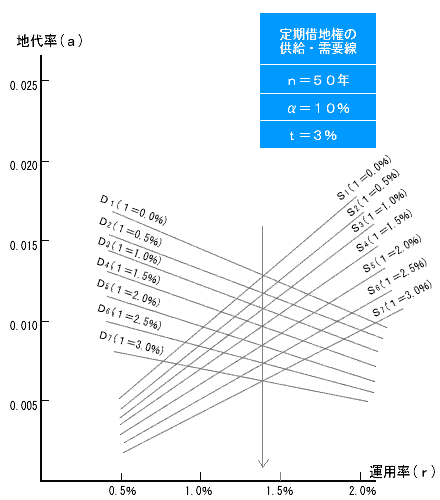
供給者サイドも需要者サイドも(r)の値を大きくしたいと考えております。 なぜなら、rの値を大きくすればするほど、供給者サイドの地代は大きくなり、需要者サイドの地代は小さくなるからです。 双方ともに、rの値を大きくしたいのですが、双方の地代(a)率は、この思惑とは裏腹にますます乖離し、全く一致点を見いだせません。 しかし、双方の方向が異なりますので、双方の思惑が一致する均衡点に向かう力が働くことになります。 従って、rの値は、供給者・需要者サイドとも同値に均衡することによって地代が決定されることになるのです。 そこで、前記により求められた供給者・需要者サイドの地代算式を使って、地代ファクター(n)(a)(i)(t)に一定値を与えて、表を作成し、供給者・需要者サイドの均衡地代を模索して見ると次の通りとなります。 ●地代ファクター
●地代率表
●均衡地代の模索 供給者サイドはrの値を上昇させれば、つまり(0.5%)から(3.0%)に上昇させれば、地代(a)率は0.351%から2.159%に増大します。 |
|